Paper – 22.10.2024
Numerical Simulation of Phase Transition with the Hyperbolic Godunov-Peshkov-Romenski Model
Our latest publication explores a new methodology to study the process of phase-transition with the continuum model of Godunov, Peshkov and Romenski.
In memory of Sergei Godunov and his groundbreaking work in the field, this paper will appear in the Journal of Computational Physics as part of a special issue In honor of Sergei Godunov.
Abstract
In this paper, a thermodynamically consistent solution of the interfacial Riemann problem for the first-order hyperbolic continuum model of Godunov, Peshkov and Romenski (GPR model) is presented. In the presence of phase transition, interfacial physics are governed by molecular interaction on a microscopic scale, beyond the scope of the macroscopic continuum model in the bulk phases. The developed two-phase Riemann solvers tackle this multi-scale problem, by incorporating a local thermodynamic model to predict the interfacial entropy production. Using phenomenological relations of non-equilibrium thermodynamics, interfacial mass and heat fluxes are derived from the entropy production and provide closure at the phase boundary.
We employ the proposed Riemann solvers in an efficient sharp interface level-set Ghost-Fluid framework to provide coupling conditions at phase interfaces under phase transition. As a single-phase benchmark, a Rayleigh-Bénard convection is studied to compare the hyperbolic thermal relaxation formulation of the GPR model against the hyperbolic-parabolic Euler-Fourier system.
The novel interfacial Riemann solvers are validated against molecular dynamics simulations of evaporating shock tubes with the Lennard-Jones shifted and truncated potential. On a macroscopic scale, evaporating shock tubes are computed for the material n- Dodecane and compared against Euler-Fourier results. Finally, the efficiency and robustness of the scheme is demonstrated with shock-droplet interaction simulations that involve both phase transfer and surface tension, while featuring severe interface deformations.
To the full Paper
https://doi.org/10.1016/j.jcp.2024.113514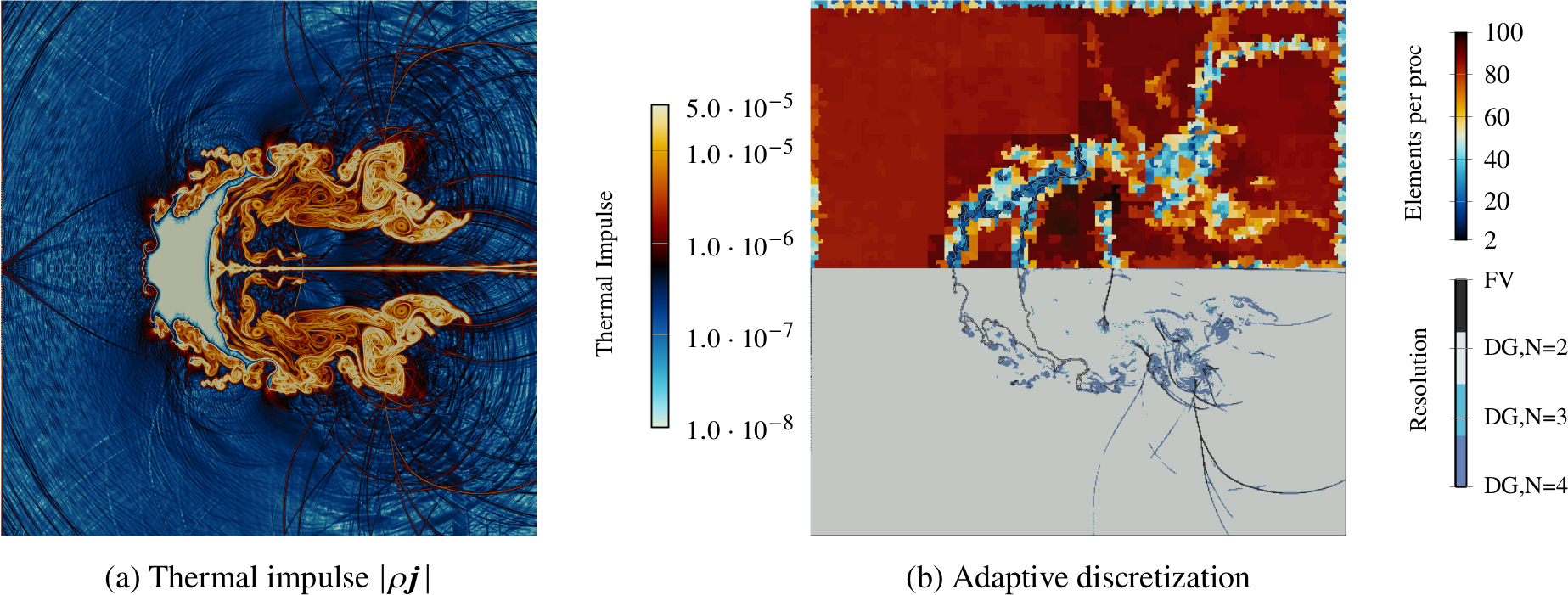
Numerical schlieren images and temperature fields of an n-Dodecane shock-droplet interaction with phase transition using the novel HLLP-mq two-phase Riemann solver (left). To obtain accurate interface localization, an hp-adaptive discretization is employed (right-top). Local workload imbalances due to the interface tracking, two-phase Riemann solver and the adaptive resolution are mitigated with a dynamic repartitioning of the domain (right-bottom).